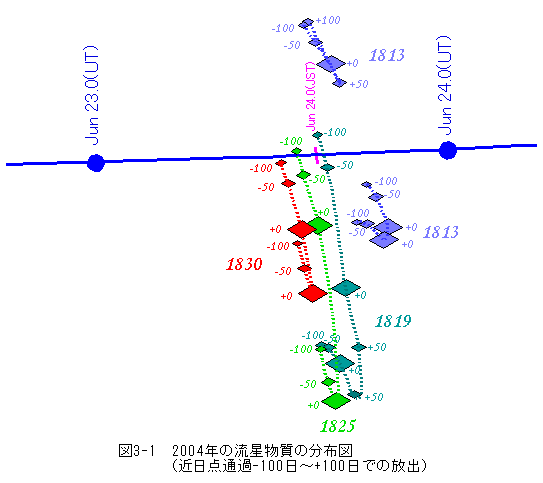
今年地球に接近する1813年、1819年、1825年、1830年放出の4トレイルについて、その近日点通過の前後からの放出の効果を計算した。±100日程度まで計算し、その位置関係を図3-3に表した。

今年接近するトレイルは複雑な構造しているため、近日点通過の瞬間からの放出では、2点(1813年においては3点)で交差する。しかし近日点通過後の放出では、回帰時期がずれてしまう。このため、図の上では近日点通過後(+側)でこれらの点が連続している。
一方近日点より前(−側)で放出させた場合は、一部で地球軌道と交差して分布することがわかった。この結果を表3-1にまとめた。また参考として、近日点通過時における放出の場合の結果を表3-2にまとめる。
| 表3-1 近日点前後放出からの結果 | ||||||||||
| 放出年 (*1) | 放出時期 [day] | 放出速度 [m/s] | 日付 | 時刻 (JST) | 太陽黄経 | 距離 [AU] | 輻射点 | 速度 [km/s] | 活動度 | |
|---|---|---|---|---|---|---|---|---|---|---|
| α | δ | |||||||||
| 1830 | -104.8 | 13.57 | 6/23 | 21:30 | 92.315 | 0 | 222.5 | 46.8 | 14.14 | 21.9% |
| 1825 | -74.7 | 12.72 | 6/23 | 22:45 | 92.365 | 0 | 222.4 | 46.8 | 14.13 | 30.4% |
| 1819 | -60.1 | 13.81 | 6/24 | 00:31 | 92.435 | 0 | 222.5 | 46.7 | 14.12 | 39.8% |
| 表3-2 近日点放出からの結果 | ||||||||||
| 放出年 (*1) | 放出時期 [day] | 放出速度 [m/s] | 日付 | 時刻 (JST) | 太陽黄経 | 距離 [AU] | 輻射点 | 速度 [km/s] | 活動度 | |
| α | δ | |||||||||
| 1830 | 0 | 8.15 | 6/23 | 22:47 | 92.366 | +0.0033 | 223.0 | 47.1 | 14.14 | 100.0% |
| 1825 | 0 | 8.83 | 6/23 | 23:47 | 92.406 | +0.0031 | 223.0 | 47.0 | 14.13 | 100.0% |
| 1819 | 0 | 10.38 | 6/24 | 01:34 | 92.477 | +0.0062 | 223.4 | 47.2 | 14.10 | 100.0% |
| 1813 | 0 | 13.29 | 6/24 | 04:34 | 92.596 | +0.0034 | 223.0 | 46.9 | 14.10 | 100.0% |
*1:母彗星の近日点通過の年を表す
今年接近するトレイルのうち、近日点の前後で放出させた場合、1819年(-60.1日)、1825年(-74.7日)、1830年(-104.8日)が地球軌道と交差することがわかった(※1813年については±約100日では交差しない)。これらについて、放出速度は近日点通過時よりは若干大きいが、十分起こりうる値であると考えられる。したがってこの条件で母彗星から放出された流星物質が存在した場合には、流星となって出現する可能性が高い。
予想される極大は、元のトレイルの接近時刻(表3-2)から推定される極大よりも、約1時間強早まることとなった。
表中の活動度は、放出された時点での太陽からの距離より求めた値で、彗星の活動度が距離の2乗に反比例すると仮定して、近日点の際と比較した。近日点から離れて放出された場合、彗星が太陽から遠いため彗星の活動度が低下し、流星物質の放出も低下すると推定される。今後流星出現規模を推定する目安となる可能性があるので、参考として掲載した。
今後は、1998年の出現の際と比較することで出現数を予想したいが、残念ながら当日までに間に合わないと思われる。もし間に合ったら報告したい。